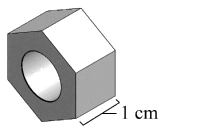
The figure above shows a metal hex nut with two regular hexagonal faces and a thickness of 1 cm. The length of each side of a hexagonal face is 2 cm. A hole with a diameter of 2 cm is drilled through the nut. The density of the metal is 7.9 grams per cubic cm. What is the mass of this nut, to the nearest gram? (Density is mass divided by volume.)
57
The question above asks students to make connections between physical concepts such as mass and density and essential geometric ideas such as the Pythagorean theorem and volume formulas. There are multiple approaches to solving this problem, but in any of them, the aim is to find the volume of the metal nut and then use the density of the metal to calculate the mass of the nut (57 grams). This is a multistep problem that requires students to devise a multistep strategy and carry out all the algebraic and numerical steps without error.
To solve this problem, students need to find the volume of the hex nut and then use the given fact that density is mass divided by volume.
Finding the volume of the hex nut requires several steps. The first step is to calculate the area of one of the hexagonal faces (without the drilled hole). Each face is a regular hexagon, which can be divided into 6 equilateral triangles with side lengths of 2 cm. Using 30-60-90 triangle properties, the height of each equilateral triangle is square root of 3 space end root cm. In turn, the area of one equilateral triangle is 0.5bh=0.5*2*((3)^0.5) square cm, so the area of the hexagonal face is
6*((3)^0.5) square cm. The volume of the hexagonal prism is the area of one face multiplied by the height (or thickness in this case), 6*((3)^0.5) *1= 6*((3)^0.5) cubic cm.
Then, to account for the drilled hole, students need to calculate the volume of a cylinder with diameter 2 cm (or radius 1 cm) and height 1 cm,
V= π(r^2)h=π(1^2)*1=π cubic cm, and subtract it from the volume of the hexagonal prism to yield 6*((3)^0.5) - π cubic cm.Finally, density is mass divided by volume, 7.9=mass/(6*((3)^0.5) - π)
the mass of the hex nut as 7.9(6*((3)^0.5) - π) grams. When the values for square root of 3 and straight pi are substituted and the result is rounded to the nearest gram, the answer is approximately 57 grams. Note that it is critical for students to attend to the precision of their calculations when solving this problem, and not apply any intermediate rounding until the final answer is reached. Here, the use of a calculator provides the ability to attend to precision more effectively, and thus is highly encouraged.
