Study Set Content:
Simplify 2(p^2)+3p+(p^2).
This expression contains two types of different terms, those that contain(p^2) and those that contain p. p2 and p are not like terms because although they contain the same letter, the letters do not have the same power.
2(p^2)+3p+(p^2)
2(p^2)+(p^2)\=3(p^2)
+3p
Putting the simplified terms together gives 3p2+3p
Click To Flip the Card
Simplify 3d×5d .
Multiply the numbers first. This gives 3×5=15
Then multiply d×d=(d^2)
The final answer is 15(d^2)
Click To Flip the Card
Expand k(k−2)
Click To Flip the Card
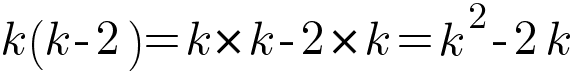
Expand 3f(5−6f)
Click To Flip the Card
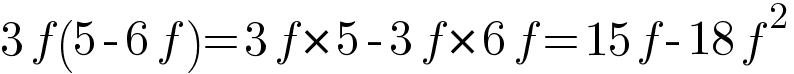
Expand the bracket (2m−3)(m+1)
Firsts = 2m×m=2(m^2)
Outsides = 2m×1=2m
Insides = −3×m=−3m
Lasts = −3×1=−3
This gives: 2(m^2)+2m−3m−3
2m and −3m
are like terms, as they both contain the letter m.
2m−3m=−1m
which can be written as −m.
Simplifying like terms gives: 2(m^2)−m−3.
Click To Flip the Card
